
트랜스포머 작동 원리를 하나하나 이해하다가 Positional Encoding은 어떻게 이루어지는지 궁금했다.
처음 이 부분을 보자마자 든 생각은 '단순히 각 시퀀스에 인덱스처럼 번호를 부여하면 될까?'였다
만약 시퀀스가 너무 길어진다면 충분히 큰 n이라는 정수값과 Input Embedding이 합쳐졌을 때와
처음 시퀀스(pos=0)와의 차이가 토큰의 의미를 상쇄해버리지 않을까라는 생각이 들었다
Positonal Encoding의 주요 목적은 다음과 같다
1.Input Embedding과 합쳐질 수 있어야한다
2.각 Position 별로 유일한 벡터가 구성되어야한다.
3.서로 다른 길이의 시퀀스의 인덱스 간격이 동일해야한다.
그럼 가장 쉽게 구현할 수 있는 인코딩부터 해보면서
가장 최선의 인코딩이 무엇인지 알아보자
Integer Encoding
| A0 "I" |
A1 "am" |
A2 "not" |
A3 "student" |
... |
| 0 | 1 | 2 | 3 | ... |
이렇게 하면 각 포지션이 독립적이면서 간격도 동일하다.
만약 첫번째 hidden layer가 $h_{i} = e_{i} + p_{i}$라면 (e = Input embedding, p= positional encoding)
A0 + 0과 300번째 시퀀스 A300 + 300은 마치 아래의 'this'와 'car'처럼 상관관계 없는 벡터에서도 상관성이 생기게 된다
즉, 단어의 의미가 아닌 위치값의 영향이 더 커지기 때문에 attention을 제대로 수행할 수 없을 것이다

참고) 각 단어 벡터(빨간색), 위치벡터(초록색)은 항상 같은 차원을 가져야한다
Normalization
포지션이 너무 커진다면 0~1사이로 정규화를 시키면 어떨까?
| A0 | A1 | A2 | A3 |
| 0 | 0.33 | 0.66 | 1 |
| B0 | B1 | B2 | B3 | B4 |
| 0 | 0.25 | 0.5 | 0.75 | 1 |
A와 B시퀀스는 각각 스케일링되었지만 A시퀀스는 임베딩 벡터 사이의 간격이 0.33이고
B시퀀스의 임베딩벡터 사이의 간격은 0.25이다. 이렇게되면 integer encoding에서
포지션 벡터가 미치는 영향이 상당 부분 감소하게된다.
하지만 문제는 Position Encoding의 주요 목표였던 각 시퀀스 간의 간격이 동일해야한다는 조건을 위반한다
A1과 B1은 두번째 Position을 가지고 있음에도 불구하고 다른 포지션으로 매핑되어 다른 위치로 인식될 것이다
즉, 같은 위치의 토큰은 같은 위치 벡터값을 가지고 있어야한다는 것이다.
Binary Encoding
이에 대한 대안으로 이진수로 각 포지션을 나타낼 수 있는데 8개의 토큰이 있다고 가정해보자.
그렇다면 3개의 벡터 ($2^{3}$)로 각 포지션을 표현할 수 있을 것이다.
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
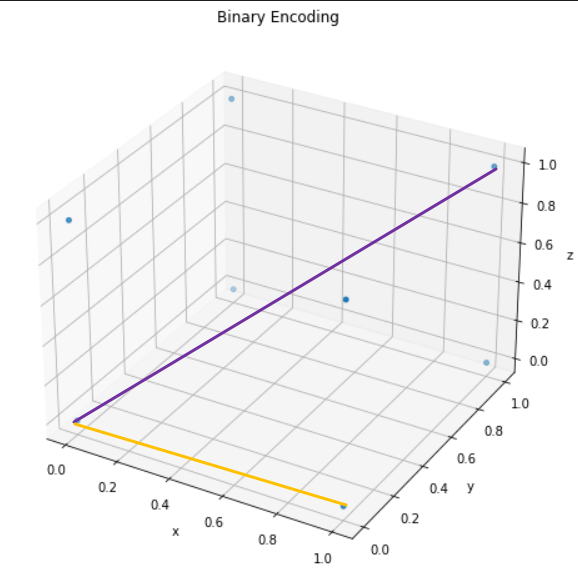
이렇게 되면 3차원 공간에서 각 포지션을 span할 수 있으며
같은 위치에 같은 벡터가 존재할 수 있다
하지만 각 벡터의 Euclidian Distance를 계산해보면
노란색 (1,0,0) 벡터와 보라색 (1,1,1) 벡터의 길이는 각각
1과 $sqrt(3)$이며, 각 벡터간의 간격이 일정하지 않음이 보인다
이는 binary dimension이 늘어날 때 각 벡터의 거리 차가
심해진다는 의미이며, 해당 방법은 적절하지 않다.
원인은 이들 벡터가 이산적(discrete)하기 때문인데,
Position Encoding은 이러한 이산적인 함수가 아니라
연속 함수에서 뽑아오는 값을 Position에 넣고싶어한다
이것도 안되고 저것도 안되면 무엇을 써야하냐!라는 느낌이 든다
앞선 과정에서 중요했던 것은 각 포지션간의 간격이 같으면서 한 방향으로 발산하지 않는 것이다.
Sigmoid
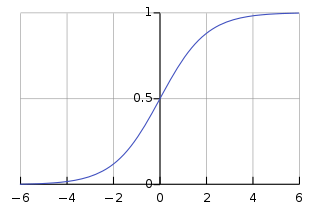
0과 1이 limitaion인 Sigmoid 함수는 어떨까?
0부터 1까지의 값을 가지기위해 증가하지만
양 끝단에서는 함수값이 바뀌지 않는다.
즉, 시퀀스가 길어질수록 각 포지션에 대한
차이 정보가 반영되기가 힘들다는 것이다
Contiuous binary vector
연속적 이진 벡터라고 해석을하면 될까 싶은데,
위에서 보았던 이진벡터 표현을 연속함수에서 가져온 버전이라고 보면된다.
그 연속함수는 바로 Sin Cos함수이다. 각 함수는 Sigmoid와 달리 -1,1을 주기적으로 순회한다.

이 함수는 긴 시퀀스에도 적절한 차이를 부여하는 포지션을 부여할 수 있다.
하지만 시퀀스 중간 중간 같은 값을 가지는 포지션이 분명히 있을 수 있다.
예를 들어 첫 시퀀스 A0가 다섯 번째 시퀀스 A4와 0이라는 동일한 벡터값을 가질 수 있다.
이 포지션 벡터들은 각각 다른 값을 가져야한다.
이를 해결하기 위해 다양한 주기를 적용시킨 sin, cos함수를 사용한다.
예를들어 nx1 벡터가 있다면 이는 n개의 주기를 가지는 벡터라고 해석할 수 있다.

위 자료가 sin cos함수로 구현한 positional encoding을 아주 잘 설명했다.
각 벡터의 가장 첫번째 차원을 sin함수로 그 차이가 크지 않게 설정하고
두번째 차원은 sin함수와 반대방향으로 움직이는 cos함수로 간격을 부여한다
이렇게 세번째와 네번째 차원을 동일하게 채워주면 각 벡터가 서로 다른 포지션을 갖게된다

식으로 정리하면 위와같은 식으로 나타낼 수 있는데, pos는 포지션이며, i는 각 벡터의 차원이다.
Attention is all you need에서는 이와같은 Position Encoding을 사용했고
PE 벡터를 트랜스포머의 다른 매트릭스와 함께 학습시켰다고 한다.
